03-01: Lexical Analysis Part 1

Token Class (or Class)

• In English: noun, verb, adjective, …
• In a programming language: identifier, keywords, <, >, numbers, …
• Token classes corresponds to sets of strings.

The goals of lexical analysis

1. Classify program substrings according to role (token class):
   • Token is a pair <token class, substrings>.
2. Communicate tokens to the parser.

03-01: Lexical Analysis Part 2

1. An implementation must do two things:
   • Recognize substring corresponding to tokens (lexemes);
   • Identify the token class of each lexeme.

03-03: Regular Languages Part 1

1. Regular Expressions:
   • Single character;
   • Epsilon (ε);
   • Union (A+B);
   • Concatenation (AB);
   • Iteration ($A\ast$).
2. The regular expression over Σ is the smallest set of expressions including:
   • $ε$
   • $c, c ∈ Σ$
   • $R + R$
   • $RR$
   • $R\ast$
3. $Σ = \{0, 1\},\ (0 + 1)\ast = Σ\ast$

03-03: Regular Languages Part 2

1. Regular expressions specify regular languages (set of strings);
2. Five constructs:
   • Two base cases (empty and 1-character strings);
   • Three compound expressions (union, concatenation, iteration).

03-04: Formal Languages

1. Let Σ be a set of characters (an alphabet). A language over Σ is a set of strings of characters drawn from Σ.
2. Meaning function L maps syntax to semantics. For regular expressions: $L: exp \to set\ of\ strings$.
3. Meaning function:
   • makes clear what is syntax, what is semantics;
   • allows us to consider notation as a separate issue;
   • because expressions and meanings are not 1-1.

04-01: Lexical Specification

Algorithm:

1. Write a regexp for the lexemes of each token class;
2. Construct $R$, matching all lexemes for all tokens;
3. Let input be $x_1 ... x_n$. For $1 \leq i \leq n$ check $x_1 ... x_i ∈ L(R)$;
4. if success, then we know that $x_1 ... x_i ∈ L(R_j)$ for some $j$;
5. Remove $x_1 ... x_i$ from input and go to 3.

Extensions:

1. Maximal munch;
2. Choose the one listed first;
3. Create rule for error strings.

04-02: Finite Automata Part 1

1. A finite automation consists of:
   • An input alphabet Σ;
   • A finite set of states S;
   • A start state n;
   • A set of accepting states F ⊆ S;
   • A set of transitions $state \to_{(input)} state$.

04-02: Finite Automata Part 2

DFA:

• One transition per input per state;
• No ε-moves.

NFA:

• Can have multiple transitions for one input in a given state;
• Can have ε-moves.

Difference:

• A DFA takes only one path through the state graph;
• An NFA can choose;
• An NFA accepts if some choices lead to an accepting state;
• DFAs are faster to execute;
• NFAs are, in general, smaller (exponentially).

04-03: Regular Expressions into NFAs

1. Algorithm:
   • Lexical Specification$\to$
   • Regular Expression$\to$
   • NFA$\to$
   • DFA$\to$
   • Table-driven implementation of DFA.
2. For each kind of regexp, define an equivalent NFA:

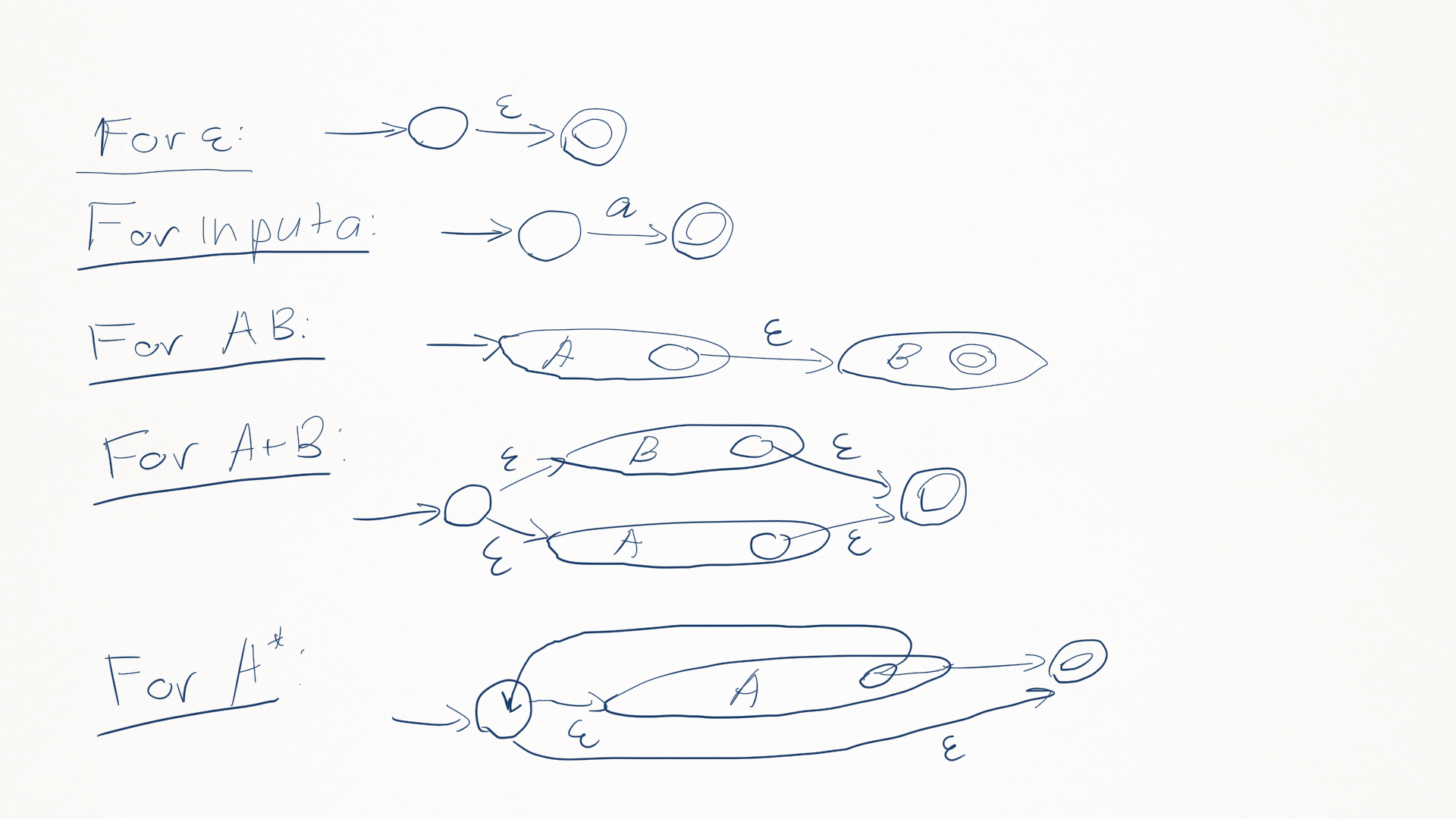
04-04: NFA to DFA

1. ε-closure of a state is all states that are reachable by ε-edge from a state.
2. DFA:
   • states: subsets of S except the empty state, S - set of states of NFA;
   • start: ε-closure(s), s - the start state of NFA;
   • final: { $X\ \vert\ X\ \cap\ F \neq 0$, F - final states of NFA };
   • trans: $X \to_{(a)} Y$ if $Y = ε-closure(\{\ y\ \vert\ x\ \in X\ and\ x\ \to_{(a)} y\ \})$.

04-05: Implementing Finite Automata

1. A DFA can be implemented by a 2D table T:
   • One dimension is states;
   • Other dimension is input symbol;
   • For every transition $s_i \to_{(a)} s_k$ define $T[i, a]=k$.